写在前面的话
熟悉的老伙伴,都知道写在前面的话,经常是题外话,不过似乎感兴趣的人更多。今天也先来点题外话。
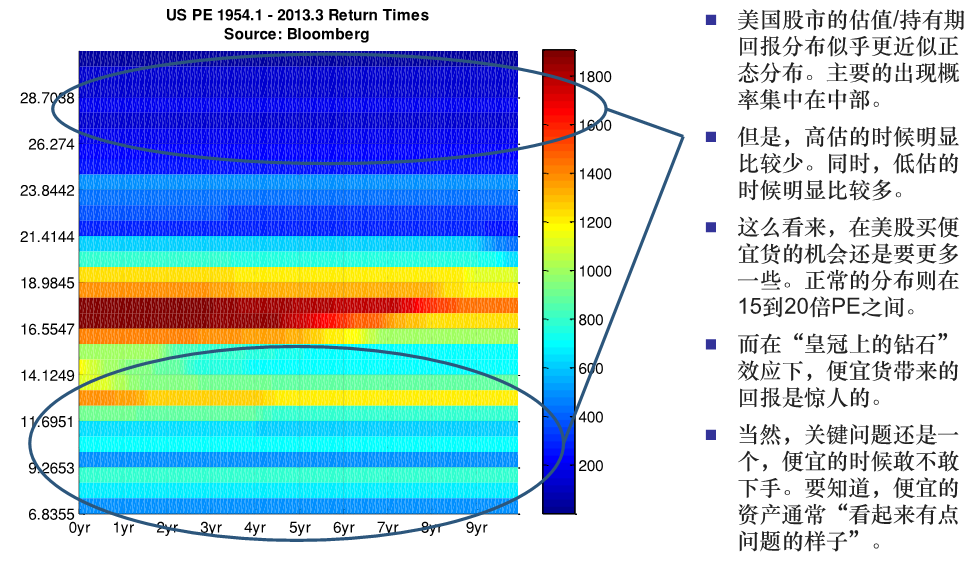
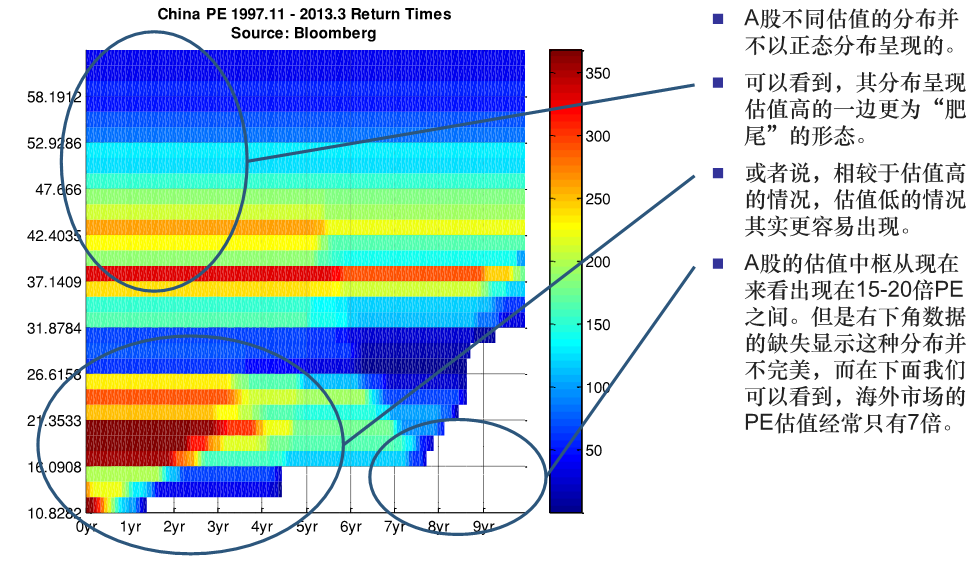
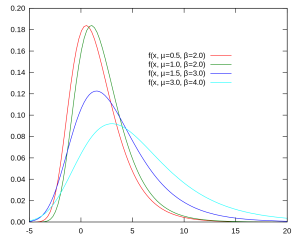
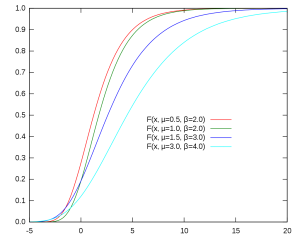
一般可以认为,活荷载、风荷载、雪荷载符合极值I型分布(Gumbel分布)。那么股市的估值会是什么分布呢?
注:这是2013年机器喵先生分析的结果。(其实A股分析存在一个问题,上证综指是失真的无法反应全市场的情况。)
感兴趣的可以继续研究一下。话说,数学的确是我们认识世界的好工具。本人惭愧,学艺不精,美好E=MC2的精神境界令人向往。
好了,回到正题。
年最大风速分布可以认为符合极值I型分布(Gumbel分布)
分布函数为
G_I(x)=e^{-e^{-y(x)}}
表示任意年份的极值xi小于任意选定值x的概率。其中,
y=\alpha(x-\mu)
\alpha=\dfrac{C_1}{\sigma}
\mu=\bar{x}-\dfrac{C_2}{\alpha}
其中,\bar{x}和σ分别为n个年度极值xi的平均值和标准差。变异系数为 \nu=\dfrac{\delta}{\bar{x}}
可以看出C1和C2其实分别就是y的标准差和平均值,它与观测序列的长度n有关。
x的年超越概率为
G(x)=1-G_I(x)
重现期为超越概率的倒数
T(x)=\dfrac{1}{G(x)}
将GI(x)带入,得
\dfrac{1}{T}=1-e^{-e^{-y}}
两侧取对数,得
y=-\ln(-ln{(1-\dfrac{1}{T}}))
可以看出,重现期T不依赖于x的均值和标准差。
另外,当T比较大时,可由泰勒展开公式简化,y≈lnT
重现期为T的最大风速x可以表达为:
x=\mu-\dfrac{y}{\alpha}
x=\bar{x}-\dfrac{\sigma}{C_1}(C_2-y)
x=\bar{x}\left(1+\dfrac{\delta}{\bar{x}}(\dfrac{y-C_2}{C_1})\right)
x=\bar{x}\left(1+\nu\dfrac{y-C_2}{C_1}\right)
设
K_{sp}=\dfrac{\nu}{C_1-C_2\nu}
则各重现期与50年重现期的转换系数可以表示为
C_{prob}=\dfrac{x_T}{x_{50}}=\dfrac{1-K_{sp}\ln(-\ln{\left(1-\dfrac{1}{T}\right))}}{1-K_{sp}\ln(-\ln{\left(1-\dfrac{1}{50}\right))}}
Cprob只与重现期T、变异系数ν、测量序列的长度n(样本年数)有关。
其中关于C1和C2的计算
可以用经验分布函数(它实际就是累积频率直方图的上边)来近似GI(x)。
y\left(x\right)=-\ln(-\ln{\left(G_I\left(x\right)\right)})
则y的值可取为1到n个zi:
z_i=-\ln(-ln\dfrac{i}{n+1})
则有
C_1=\sigma_z=\dfrac{1}{n}\sum_{i=1}^{n}{(z_i-\bar{z})}^2=\dfrac{1}{n}\sum_{i=1}^{n}{z_i^2-{\bar{z}}^2}
C_2=\bar{z}
当n无限大时, C_1=\dfrac{\pi}{\sqrt{6}} , C_2=0.57722 (为欧拉常量)
工程实践中各重现期风速与50年重现期的转换可以参考以下情况:
1. 在EN50341-1中,采用上面的推导的公式,其中风速的变异系数取0.12,观测数据取30年,则Ksp=0.114。转换系数为
C_{prob}=0.692-0.079ln(-ln(1-\dfrac{1}{T}))
2. 在ASCE7中,根据文献Peterka, J.A., and Shahid, S. (1998). Design gust wind speeds in the United States. J. Struct. Eng. 124(2), 207–214.。对于非飓风区转换系数为
C_{prob}=0.36+0.10ln(12T)
3. 在中国规范中,根据文献《结构风工程:理论规范实践》。转换系数为
C_{prob}=\sqrt{\dfrac{(0.363log{T}+0.463)}{1.08}}
4. 在EN1991-1-4中,风压的变异系数取24,观测数据取无穷。转换系数为
C_{prob}=\sqrt{0.562-0.112ln(-ln(1-\dfrac{1}{T}))}
(P.S. 对于Euorcode1的如此处理本人存疑?长重现期的风速会明显偏小。有知道原因的大神可以来讲讲)
各重现期风速与50年重现期的转换系数如下所示
| 重现期 | EN50341-1, ν=0.12 | GB | ASCE7 | EN1991-1-4 |
| 3 | 0.76 | 0.77 | 0.72 | 0.81 |
| 50 | 1.00 | 1.00 | 1.00 | 1.00 |
| 100 | 1.06 | 1.05 | 1.07 | 1.04 |
| 150 | 1.09 | 1.08 | 1.11 | 1.06 |
| 200 | 1.11 | 1.10 | 1.14 | 1.08 |
| 300 | 1.14 | 1.12 | 1.18 | 1.10 |
| 400 | 1.17 | 1.14 | 1.21 | 1.11 |
| 500 | 1.18 | 1.16 | 1.23 | 1.12 |
| 600 | 1.20 | 1.17 | 1.25 | 1.13 |
| 700 | 1.21 | 1.18 | 1.26 | 1.14 |
| 800 | 1.22 | 1.19 | 1.28 | 1.15 |
| 900 | 1.23 | 1.19 | 1.29 | 1.15 |
| 1000 | 1.24 | 1.20 | 1.30 | 1.16 |
小知识:设计基准期、重现期、设计使用年限间的关系。
重现期T为某事件出现或发生的平均时间间隔。
设计基准期N(是衡量基准,选定后不变,一般为50年)内的超越概率为
P_N=1-(1-\dfrac{1}{T})N
若年超越概率2%即重现期T=50年,设计基准期N=50年,则PN=63%
设计使用年限L(根据业主要求确定,一般为50年或100年)内的超越概率为
P_L=1-(1-\dfrac{1}{T})L
移项后两边取对数
ln(1-\dfrac{1}{T})=\dfrac{ln(1-P_L)}{L}
当T较大时,由泰勒展开公式, ln(1-\dfrac{1}{T})\approx-\dfrac{1}{T}
T≈-\dfrac{L}{ln(1-P_L)}
令,设计使用年限L内的超越概率与50年设计基准期内的超越概率具有相同的水平
T\approx-\dfrac{L}{ln(1-63\%)}
则有T≈L,即重现期可取为与设计使用年限相同。
例如设计使用年限取100年时,对于风载采用100年重现期的风荷载即可。